들어가기 전에
분할 정복식 알고리즘 : 하향식 해결법으로서, 나누어진 부분들 사이에 서로 상관관계가 없는 문제를 해결하는데 적합하다. ( ex)피보나치 알고리즘의 재귀)
동적계획
상향식 해결법을 사용하여 알고리즘을 설계하는 방법이다. 이 방법은 분할정복식 방법과 마찬가지로 문제를 나눈 후에 나누어진 부분들을 먼저 푼다. 그러나 이미 풀어서 답을 알고 있는 부분의 결고가 다시 필요한 경우에는 반복하여 계산하는 대신에 이미 계산된 결과를 그냥 사용한다.
-> 작은 문제의 답을 저장했다가 사용
개발 절차
1. 문제의 사례에 대해서 해답을 주는 재귀 관계식(recursive property)을 정립한다.
2. 작은 사례를 먼저 해결하는 상향식 방법으로 문제의 사례를 해결한다.
예제1) 피보나치 수 구하기
-분할 정복식,재귀
int fib(int n) {
if (n <= 1) return n;
else
return fib(n - 1) + fib(n - 2);
}-> 재귀 알고리즘은 같은 피보나치 수를 중복 계산하여 수행속도가 매우 느리다.
( ex) fib(5)계산에 fib(2)를 3번 중복 계산)
-동적 계획
int fib(int n) {
int f[N];
f[0] = 0;
if (n > 0) {
f[1] = 1;
for (int i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
}
return f[n];
}
예제2) 이항계수(Binomial Coefficient) 구하기
이항계수란? 조합론에서 등장하는 개념으로 주어진 크기 집합에서 원하는 개수만큼 순서없이 뽑는 조합의 가짓수
-전체 집합에서 원소의 개수 n에 대해 k개의 아이템을 뽑는 이항계수(조합의 수)는
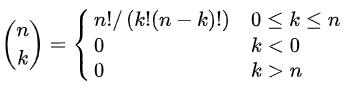
-이항계수 점화식
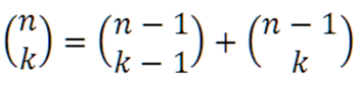
설명: 원소가 {1,2,3,4}인 집합에서 3개를 뽑는 상황-> 4C3
위의 상황에서 먼저 원소 1에 대한 선택 여부를 고려한다 했을 때
원소 1를 선택: 나머지 3개 중에서 2개를 선택->3C2
원소 1를 선택하지 않은 경우: 나머지 3개 중에서 3개를 선택->3C3
-> 4C3 = 3C2 + 3C3
-파스칼의 삼각형
:이항계수를 구하는 또 다른 방법
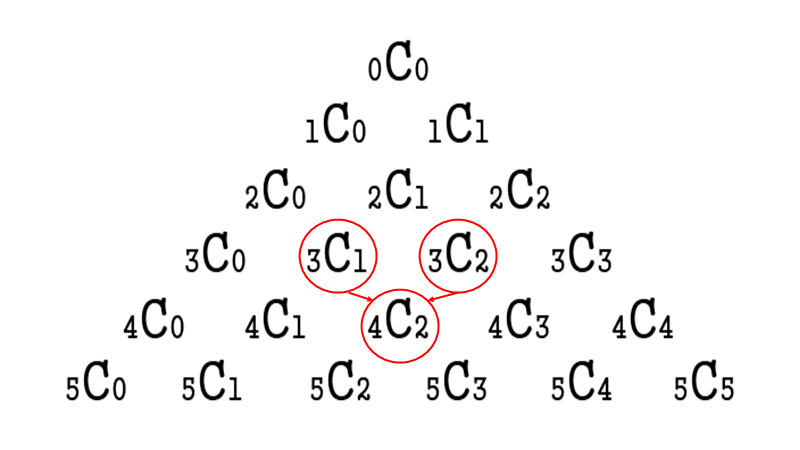
->4C2 = 3C1 + 3C2
-분할 정복식
int bin(int n,int k) {
if (n == k || k == 0)
return 1;
else
return bin(n - 1, k) + bin(n - 1, k - 1);
}
-동적 계획식
재귀 관계식 정립
:2차원 배열 B를 만들고 각 B[n][k]에는 (n k)값을 저장하도록 하면, 그 값은 다음과 같은 관계식으로 계산할 수 있다.
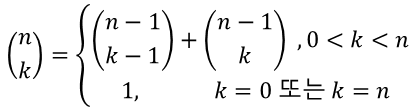
↓
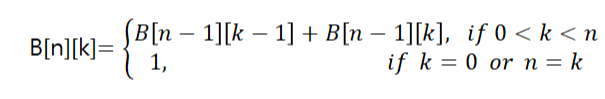
int bin(int n,int k) {
int B[n][k] = { 0, }; //크기를 상수로 넣어주기
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= min(i,k); j++) {
if (j == 0 || i == j)
B[i][j] = 1;
else
B[i][j] = B[i - 1][j - 1] + B[i - 1][j];
}
}
return B[n][k];
}'Algorithm > 자료구조' 카테고리의 다른 글
| [자료구조] DFS와 BFS (0) | 2021.02.24 |
|---|---|
| [자료구조] 그래프 (0) | 2021.02.24 |
| [c++ / STL] sort, priority queue (0) | 2021.01.30 |
| [자료구조] 정렬 , 우선순위 큐(힙정렬) (0) | 2021.01.30 |
| [자료구조] [c++/STL] 스택, 큐, 덱 (0) | 2021.01.27 |
